A fundamental truth for SQL Server’s optimizer

Table joins vs. query plans

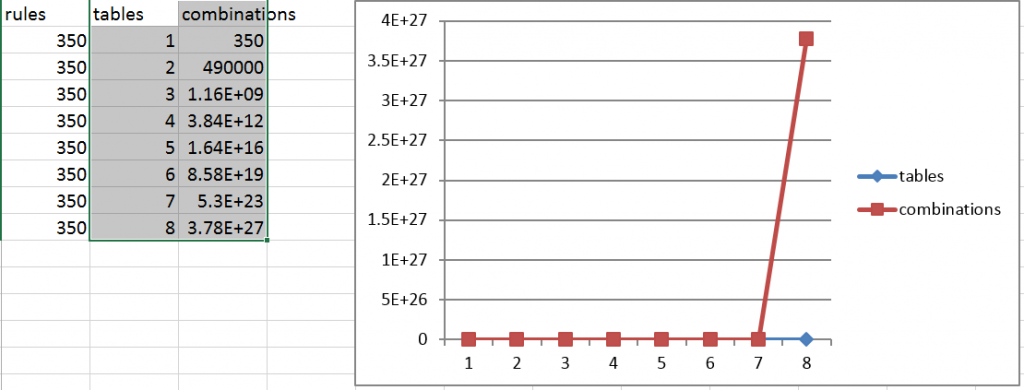
SQL Server uses an optimizer to figure out how to retrieve data and process a query. For every table, it evaluates roughly 350 different rules. It occurred to me that this would lead to exponential growth in the number of potential query plans. The following formula is one way to think about the problem of increasing the potential number of query plans as the number of tables in a query increases:

(t*350)^t

In the above query, ‘t’ represents the number of tables. It’s obvious that the optimizer would need to evaluate 350 rules per table (hence t*350). That’s actually not always true as the optimizer knows how to take some shortcuts, but it’s a reasonable number for this exercise. What’s less obvious is that the order that the optimizer evaluates rules for tables increases exponentially with the number of tables. This is expressed by the part of the formula that raises the result of the rules evaluation for each table to the power of the number of tables (^t). It turns out that this is an ‘NP complete’ problem.

What this means in the real world is that it quickly becomes less likely that  SQL Server’s optimizer will find the optimal execution plan once you have more than 6 tables in a join. That doesn’t mean that performance will always be awful with more that 6 tables in a join. It just means that it becomes much more likely. Once you encounter performance problems with this many tables in a query, there may be no other way to improve performance than to reduce the number of tables joined.